Ökosysteme sind in der Regel probabilistische, d.h. stochastische Systeme. Sie sind es deshalb, weil sie zum einen von einer Vielzahl unterschiedlicher Parameter abhängig sind, von denen man zwar die wichtigsten, aber nie alle erfassen kann, und zum anderen, weil sie stets offen sind. Ihre wichtigsten Glieder, die Organismen, sind nämlich auf ständige Energiezufuhr angewiesen. Es gibt daher zwei konzeptionell verschiedene Verfahren, um Informationen über Lebensgemeinschaften und Ökosysteme zu gewinnen.
1. Bestandsaufnahmen:
| Erfassung von (allen) Arten eines Lebensraums, | |
| Ermittlung der prozentualen Anteile der einzelnen Arten, | |
| Bestimmung von Veränderungen der Artenzusammensetzung (und Individuenzusammensetzung) als Funktion der Zeit (a. im Jahreszyklus; b. über längere Zeiträume hinweg), | |
| Bestimmung und Registrierung aller chemischen und physikalischen Parameter, von denen die Existenz der Organismen abhängt. |
Bestandsaufnahmen haben eine lange Tradition. Hier sollen sie vorweg nur durch Stichworte wie Vegetationskartierung und Pflanzengeographie gekennzeichnet sein, mehr dazu im Thema Pflanzengesellschaften.
2. Systemanalytischer Ansatz:
Der systemanalytische Ansatz ist jüngeren Datums. Mit dem Aufkommen der Kybernetik Mitte der vierziger Jahre wurden Hilfsmittel erarbeitet, um Systeme und Systemeigenschaften mathematisch zu definieren und um zum Prognostizieren geeignete Modelle zu konzipieren.
Beide Ansätze - Bestandsaufnahme und Systemtheorie - ergänzen einander, und nur unter Berücksichtigung der Ergebnisse beider läßt sich der Versuch unternehmen, ein Ökosystem zu verstehen und sein Verhalten, seine Gleichgewichtslage und die Empfindlichkeit gegenüber Störungen zu beschreiben sowie zukünftige Entwicklungen zu erkennen.
Grundlagen der Systemtheorie werden im Thema Kybernetik besprochen, hier einige Ergänzungen sowie eine Veranschaulichung anhand eines Beispiels.
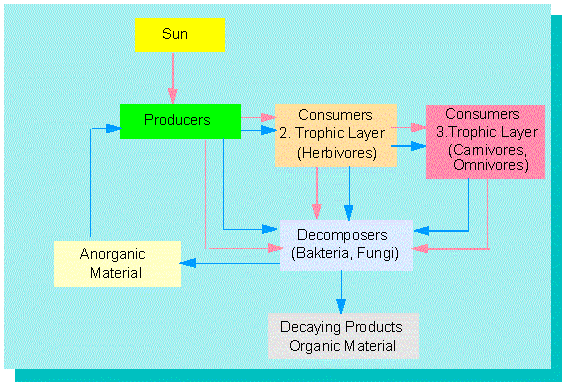
Vereinfachtes Modell eines Energie- und Materialflusses in einem Ökosystem. Der Materialfluß (blaue Linien) ist ein Kreislauf, der Energiefluß (rote Linien) ein linearer.
Die Systemelemente (hier Produzenten, Konsumenten erster Ordnung, Konsumenten zweiter Ordnung, Zersetzer) sind hintereinander angeordnet. Die Anordnung ist hierarchisch. Die einzelnen Hierarchieebenen werden als Trophiebenen bezeichnet.
Es gibt einen Energie- und einen Materialfluß zwischen den Systemelementen. Der Energiefluß ist ein linearer Prozeß; der Materialfluß stellt einen Kreislauf dar.
Nur Pflanzen (und wenige Mikroorganismen) können Lichtenergie in chemische Energie umsetzen. Man nennt sie daher Produzenten (Primärproduzenten, P). Alle übrigen Organismen sind Konsumenten (1., 2., 3. Ordnung) oder Zersetzer (Saprophyten). Die Lebensweise der Produzenten bezeichnet man als autotroph, die der Konsumenten als heterotroph (Autotrophie, Heterotrophie). Für eine mathematische Beschreibung eines Ökosystems benötigt man nunmehr vier Grundelemente:
1. Systemvariable (vi): Darunter versteht man eine Gruppe von Werten (v1, v2 ... vn), durch die der Zustand eines Systems zu einem gegebenen Zeitpunkt beschrieben wird. Dazu gehören beispielsweise die Angaben über die Biomasse (ausgedrückt in g, kg oder t Trockengewicht pro Flächen- oder Volumeneinheit). Den Produzenten (P) käme demnach der Wert v1, den Konsumenten 1. Ordnung der Wert v2, den Konsumenten 2. Ordnung (Carnivoren der Wert v3 usw. zu.
2. Transfer- oder Übergangsfunktionen (Fi): Das sind Gleichungen, die den Stoffumsatz im System beschreiben. Unter anderem wird durch sie der Anteil an Biomasse erfaßt, der durch Veratmung verlorengeht, oder jener, der zur Ernährung der Individuen in einer übergeordneten Trophieebene benötigt wird (s. folgenden Abschnitt). Die Veränderungen einer Systemvariablen als Funktion der Zeit wäre demnach durch die folgende Differentialgleichung zu beschreiben
dvi / dt = f (v1, v2.......... vn, F1, F2... Fn)
wobei f hier ganz allgemein für Funktion steht.
3. Antriebsfunktionen (inputs): Darunter wird die Energie- und Materialmenge verstanden, die einem System zur Verfügung steht, zum Beispiel die Menge der eingestrahlten, verwertbaren Sonnenenergie, die limitierende Menge an Nährstoffen (Mineralien) im Boden, die Temperatur als reaktionsbestimmender Faktor usw. Möchte man nur die Transferfunktion von einer trophischen Stufe zur nächst höheren betrachten, wird das entsprechende Fi zur Antriebsfunktion. Für die Menge an Carnivoren beispielsweise ist die der Herbivoren (und der Carnivoren) ausschlaggebend.
4. Proportionalitätsfaktoren (ci), konstante Parameter: Dieser Kategorie gehören unveränderliche Größen an, beispielsweise die Menge pflanzlicher Nahrung, die ein einzelnes Tier pro Zeiteinheit benötigt.
Das mathematische Modell eines Systems ist nunmehr als ein Satz von Gleichungen zu schreiben, die den Energie- und Materialfluß zwischen den einzelnen Ebenen (Stufen) beschreiben. Zur Verrechnung von Datensätzen und Gleichungen bedient man sich heutzutage der Matrizenrechnung. Eine Matrix ist zunächst einmal nichts anderes als eine Datenliste, in der jeder Wert durch seine Koordinaten i und j gekennzeichnet ist. Matrices sind untereinander multiplizierbar, wobei als Ergebnis wiederum eine Matrix entsteht. Mit einer solchen Darstellung läßt sich zum Beispiel zeigen, welche Gruppe (Systemkomponente) direkten Einfluß auf eine andere hat. Auf unser generalisiertes Ökosystem bezogen, ergibt sich dann ein Bild, aus dem zu ersehen ist, daß jede Systemkomponente auf sich selbst einwirkt, daß aber beispielsweise die Carnivoren keinen direkten Einfluß auf die Pflanzen ausüben.
In der ökologischen Forschung fallen stets große Datenmengen an. Es ist daher sinnvoll, sie computergerecht aufzuarbeiten, d.h., sie von vornherein so in Matrices zu ordnen, daß sie für eine Eingabe in den Rechner geeignet sind. Bei der Beurteilung natürlicher Ökosysteme ist zu berücksichtigen, daß die Realität oft von idealisierten Modellvorstellungen abweicht. Für viele der benötigten Parameter lassen sich keine exakten Datensätze gewinnen. In der Regel sind die Antriebsfunktionen großen Schwankungen unterworfen, so zum Beispiel den nicht vorhersagbaren Witterungsbedingungen. Die Zahl der Wechselwirkungen in einem natürlichen Ökosystem ist meist größer als im Modell. Um auf unser Beispiel zurückzugreifen, sei vermerkt, daß sich Tiere keineswegs klar in Herbivoren und Carnivoren einteilen lassen, denn viele sind bekanntlich Allesfresser (Omnivoren). Doch wenn man solche Komplikationen kennt, lassen sie sich unschwer in ein vorhandenes Modell integrieren. Oft fehlt es jedoch an der notwendigen Information. Andererseits gibt es aber auch Beziehungen, die quantitativ kaum ins Gewicht fallen. Es ist daher sinnvoll, sie zu vernachlässigen, um sich nicht mit unnötiger Rechenarbeit zu belasten.
Man kannte bislang nur sehr wenige Ökosysteme, an denen beispielhaft gezeigt werden konnte, welche Eigenschaften das System hat. Es gibt in Deutschland einen See, den Plußsee bei Plön/Holst., der als ein Beispiel für ein nahezu vollkommen erforschtes Ökosystem zitiert werden kann (bearbeitet vom Max-Planck-Institut für Limnologie in Plön). Als Beispiel für ein terrestrisches System kann das "Solling-Projekt" erwähnt werden, ein Waldgebiet, das von Wissenschaftlern der Universität Göttingen untersucht wird.
Die Mehrzahl ökologisch arbeitender Biologen verfügt zwar meist über die notwendige Kenntnis der Pflanzen- und / oder Tierarten, doch nur sehr wenige wissen etwas über Bodenbakterien und -pilze (Zersetzer). Es gibt daher kaum Daten über deren Artzusammensetzung, Populationsdichte und Vermehrungsrate in ihrer natürlichen Umwelt. Vermehrungskinetiken, die unter Laborbedingungen gemessen wurden, sind nur bedingt brauchbar, weil die Wachstumsbedingungen dort meist günstiger sind und die Vermehrungsrate damit höher liegt als in der Natur.
Systemanalytische Ansätze lassen sich jedoch oft derart perfektionieren, daß man mit nur wenig, dazu auch noch recht lückenhafter Information relativ treffsichere Vorhersagen machen kann. Zur Illustration sei auf die Hochrechnungen nach Bundes- und Landtagswahlen verwiesen, deren erste Prognosen dem amtlichen Endergebnis in der Regel schon sehr nahe kommen. Auch in der Ökologie ist man auf vergleichbare Optimierungsprozesse angewiesen, denn alle Datenlisten, so umfangreich sie auch aussehen mögen, repräsentieren immer nur eine verhältnismäßig kleine Stichprobe der tatsächlich vorhandenen, doch nicht erfaßten Daten. Mit zunehmender Komplexität eines mathematischen Modells nimmt seine Treffsicherheit zu, mit zunehmender Komplexität eines Ökosystems steigt - wie schon gesagt - auch dessen Stabilität. Aus der Statistik wissen wir, daß ein systematischer Fehler (s) umgekehrt proportional zur Wurzel aus der Zahl der Einzelmessungen ist (1/ Wurzel n). Je größer das Zahlenmaterial ist, desto geringer ist folglich die Fehlerquote.
© Peter v. Sengbusch - b-online@botanik.uni-hamburg.de